Wavelet routine for local multiple correlation — wave.local.multiple.correlation • wavemulcor

Produces an estimate of the multiscale local multiple correlation (as defined below) along with approximate confidence intervals.

wave.local.multiple.correlation(xx, M, window="gauss", p = .975, ymaxr=NULL)

Arguments

xx	A list of \(n\) (multiscaled) time series, usually the outcomes of dwt or modwt, i.e. xx <- list(v1.modwt.bw, v2.modwt.bw, v3.modwt.bw)
M	length of the weight function or rolling window.
window	type of weight function or rolling window. Six types are allowed, namely the uniform window, Cleveland or tricube window, Epanechnikov or parabolic window, Bartlett or triangular window, Wendland window and the gaussian window. The letter case and length of the argument are not relevant as long as at least the first four characters are entered.
p	one minus the two-sided p-value for the confidence interval, i.e. the cdf value.
ymaxr	index number of the variable whose correlation is calculated against a linear combination of the rest, otherwise at each wavelet level wlmc chooses the one maximizing the multiple correlation.

Details

The routine calculates one single set of wavelet multiple correlations out of \(n\) variables that can be plotted in in either single heatmap or \(J\) line graphs (the former is usually the best graphic option but the latter is useful if confidence intervals are explicitly needed), as an alternative to trying to make sense out of \(n(n-1)/2\) \([J \times T]\) sets of local wavelet correlations. The code is based on the calculation, at each wavelet scale, of the square root of the coefficient of determination in that linear combination of locally weighted wavelet coefficients for which such coefficient of determination is a maximum. The code provided here is based on the wave.multiple.correlation routine in this package which in turn is based on the wave.correlation routine in Brandon Whitcher's waveslim R package Version: 1.6.4, which in turn is based on wavelet methodology developed in Percival and Walden (2000); Gençay, Selçuk and Whitcher (2001) and others.

Value

List of four elements:

val:

numeric matrix (rows = #observations, columns = #levels in the wavelet transform object) providing the point estimates for the wavelet local multiple correlation.

lo:

numeric matrix (rows = #observations, columns = #levels in the wavelet transform object) providing the lower bounds from the confidence interval.

up:

numeric matrix (rows = #observations, columns = #levels in the wavelet transform object) providing the upper bounds from the confidence interval.

YmaxR:

numeric matrix (rows = #observations, columns = #levels in the wavelet transform object) giving, at each wavelet level and time, the index number of the variable whose correlation is calculated against a linear combination of the rest. By default, wlmc chooses at each wavelet level and value in time the variable maximizing the multiple correlation.

References

Fernández-Macho, J., 2018. Time-localized wavelet multiple regression and correlation, Physica A: Statistical Mechanics, vol. 490, p. 1226--1238. <DOI:10.1016/j.physa.2017.11.050>

Note

Needs waveslim package to calculate dwt or modwt coefficients as inputs to the routine (also for data in the example).

Examples


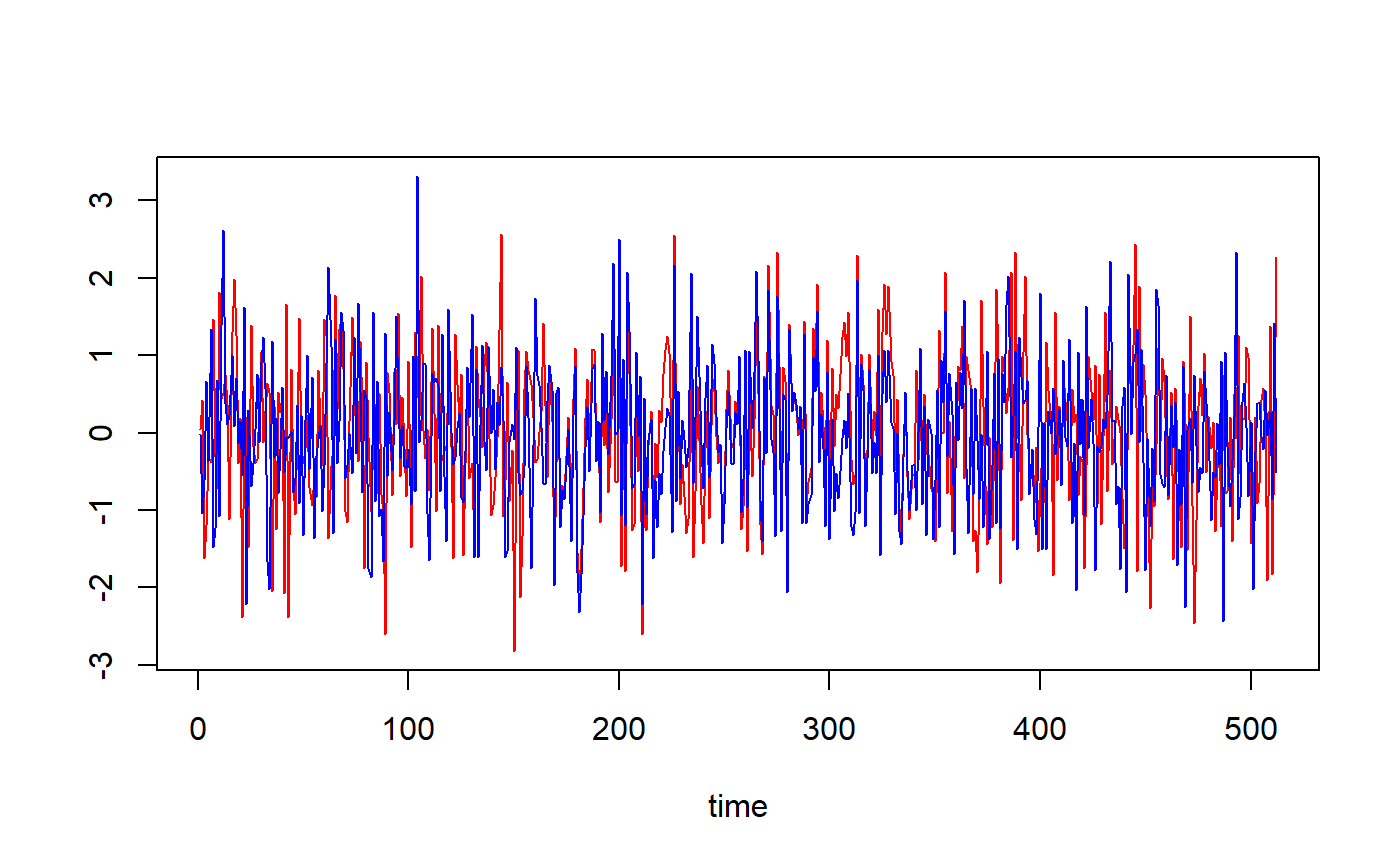
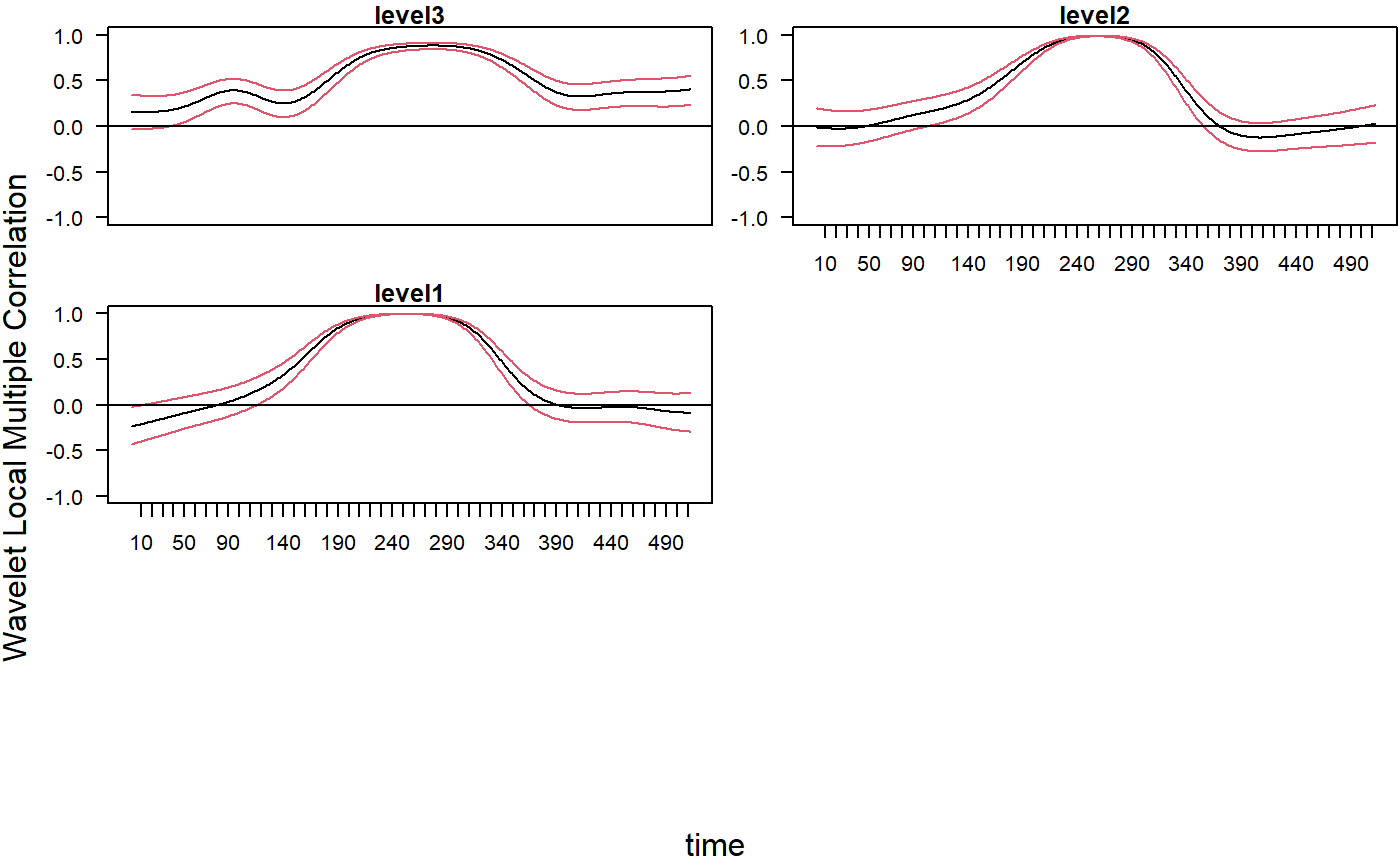
## Based on  Figure 4 showing correlation structural breaks in Fernandez-Macho (2018).

library(wavemulcor)
options(warn = -1)

data(xrand)
N <- length(xrand1)
b <- trunc(N/3)
t1 <- 1:b
t2 <- (b+1):(2*b)
t3 <- (2*b+1):N

wf <- "d4"
M <- N/2^3 #sharper with N/2^4
window <- "gauss"
J <- 3 #trunc(log2(N))-3

# ---------------------------

cor1 <- cor(xrand1[t1],xrand2[t1])
cor2 <- cor(xrand1[t2],xrand2[t2])
cor3 <- cor(xrand1[t3],xrand2[t3])
cortext <- paste0(round(100*cor1,0),"-",round(100*cor2,0),"-",round(100*cor3,0))

ts.plot(cbind(xrand1,xrand2),col=c("red","blue"),xlab="time")

xrand1.modwt <- modwt(xrand1, wf, J)
xrand1.modwt.bw <- brick.wall(xrand1.modwt, wf)

xrand2.modwt <- modwt(xrand2, wf, J)
xrand2.modwt.bw <- brick.wall(xrand2.modwt, wf)

xx <- list(xrand1.modwt.bw,xrand2.modwt.bw)

# ---------------------------

xy.mulcor <- wave.local.multiple.correlation(xx, M, window=window)
#> 
#> lev:1234

val <- as.matrix(xy.mulcor$val)
lo  <- as.matrix(xy.mulcor$lo)
up  <- as.matrix(xy.mulcor$up)
YmaxR <- as.matrix(xy.mulcor$YmaxR)

# ---------------------------

old.par <- par()

# ##Producing heat plot

scale.names <- paste0("(",c("2-4","4-8","8-16","16-32","32-64","64-128","128-256","256-512",
                            "512-1024","1024-2048"),"]")
scale.names <- c(scale.names[1:J],"smooth")

title <- paste("Wavelet Local Multiple Correlation")
sub <- paste("first",b,"obs:",round(100*cor1,1),"% correlation;","middle",b,"obs:",
             round(100*cor2,1),"%","rest:",round(100*cor3,1),"%")
xlab <- "time"
ylab <- "periods"

plot3D::image2D(z=val, x=1:nrow(val), y=1:ncol(val),
        main=title, #sub=sub,
        xlab=xlab, ylab=ylab, axes=FALSE, clab = expression(varphi),
        rasterImage = TRUE, contour = list(lwd = 2, col = plot3D::jet.col(11)))
axis(side=1, at=seq(10,nrow(val),by=10), cex.axis=0.75)
axis(side=2, at=1:ncol(val),labels=scale.names, las=1,cex.axis=0.75)

# ---------------------------

##Producing line plots with confidence intervals

colnames(val)[1:J] <- paste0("level",1:J)
par(mfrow=c(3,2), las=1, pty="m", mar=c(2,3,1,0)+.1, oma=c(1.2,1.2,0,0))
for(i in J:1) {
  matplot(1:N,val[,i], type="l", lty=1, ylim=c(-1,1), xaxt="n",
          xlab="", ylab="", main=colnames(val)[i])
  if(i<3) {axis(side=1, at=seq(10,N,by=10))}
  #axis(side=2, at=c(-.2, 0, .5, 1))
  lines(lo[,i], lty=1, col=2) ##Add Connected Line Segments to a Plot
  lines(up[,i], lty=1, col=2)
  abline(h=0)              ##Add Straight horiz and vert Lines to a Plot
}
par(las=0)
mtext('time', side=1, outer=TRUE, adj=0.5)
mtext('Wavelet Local Multiple Correlation', side=2, outer=TRUE, adj=0.5)

#reset graphics parameters
par(old.par)