Routine for local multiple regression

Produces an estimate of local multiple regressions (as defined below) along with approximate confidence intervals.

local.multiple.regression(xx, M, window="gauss", p=.975, ymaxr=NULL)

Arguments

xx	A list of \(n\) time series, e.g. xx <- list(v1, v2, v3)
M	length of the weight function or rolling window.
window	type of weight function or rolling window. Six types are allowed, namely the uniform window, Cleveland or tricube window, Epanechnikov or parabolic window, Bartlett or triangular window, Wendland window and the gaussian window. The letter case and length of the argument are not relevant as long as at least the first four characters are entered.
p	one minus the two-sided p-value for the confidence interval, i.e. the cdf value.
ymaxr	index number of the variable whose correlation is calculated against a linear combination of the rest, otherwise at each wavelet level lmc chooses the one maximizing the multiple correlation.

Details

The routine calculates a set of time series of multiple regression coeffcients out of \(n\) variables.

Value

List of four elements:

cor:

List of three elements:

val: numeric vector (rows = #observations) of point estimates for the local multiple correlation. lo: numeric vector (rows = #observations) of lower bounds of the confidence interval. up: numeric vector (rows = #observations) of upper bounds of the confidence interval.

reg:

List of seven elements:

rval: numeric matrix (rows = #observations, cols = #regressors+1) of local regression estimates. rstd: numeric matrix (rows = #observations, cols = #regressors+1) of their standard deviations. rlow: numeric matrix (rows = #observations, cols = #regressors+1) of their lower bounds. rupp: numeric matrix (rows = #observations, cols = #regressors+1) of their upper bounds. rtst: numeric matrix (rows = #observations, cols = #regressors+1) of their t statistic values. rord: numeric matrix (rows = #observations, cols = #regressors+1) of their index order when sorted by significance. rpva: numeric matrix (rows = #observations, cols = #regressors+1) of their p values.

YmaxR:

numeric vector (rows = #observations) giving, at each value in time, the index number of the variable whose correlation is calculated against a linear combination of the rest. By default, lmr chooses at each value in time the variable maximizing the multiple correlation.

data:

dataframe (rows = #observations, cols = #regressors) of original data.

References

Fernández-Macho, J., 2018. Time-localized wavelet multiple regression and correlation, Physica A: Statistical Mechanics, vol. 490, p. 1226--1238. <DOI:10.1016/j.physa.2017.11.050>

Examples

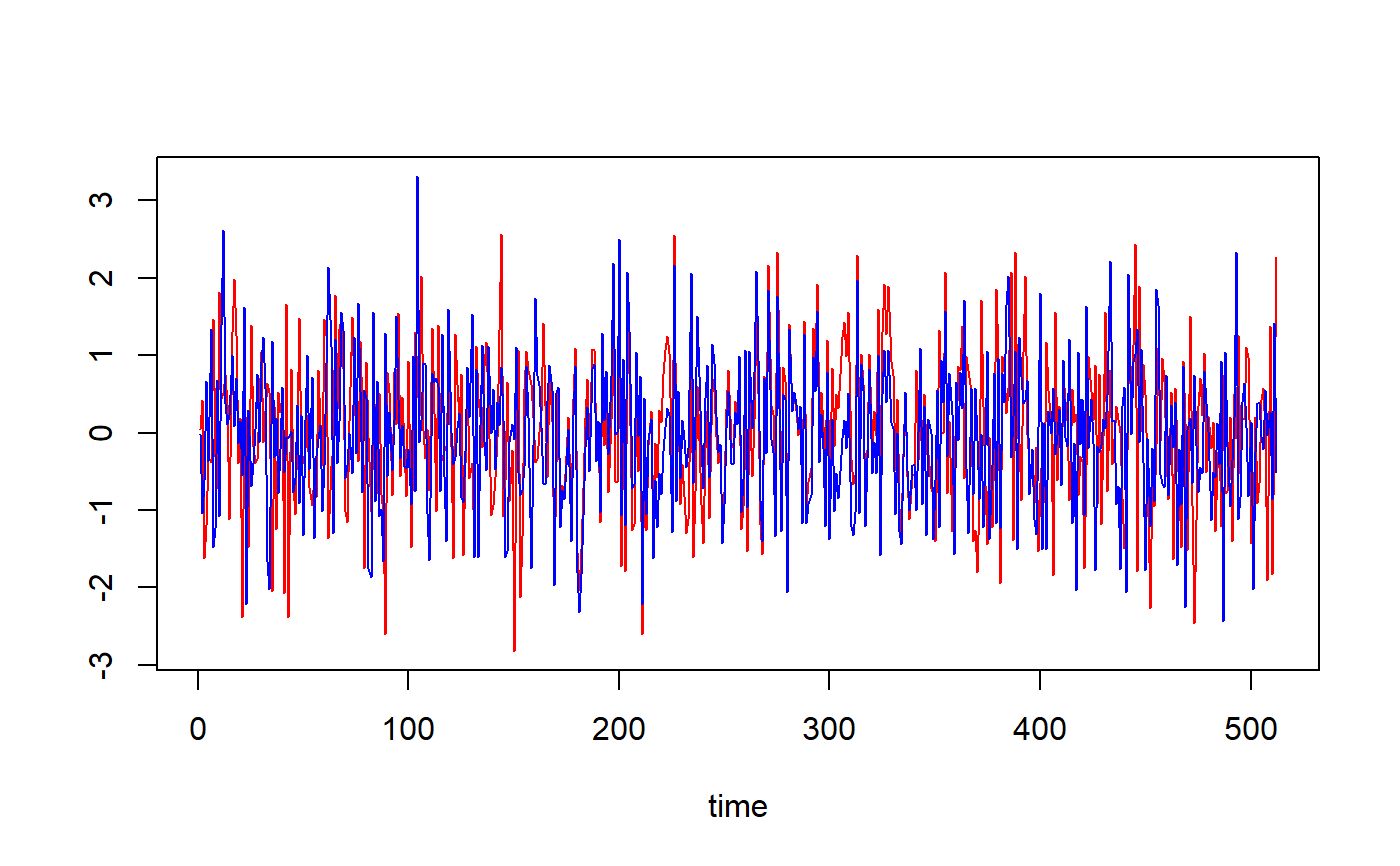
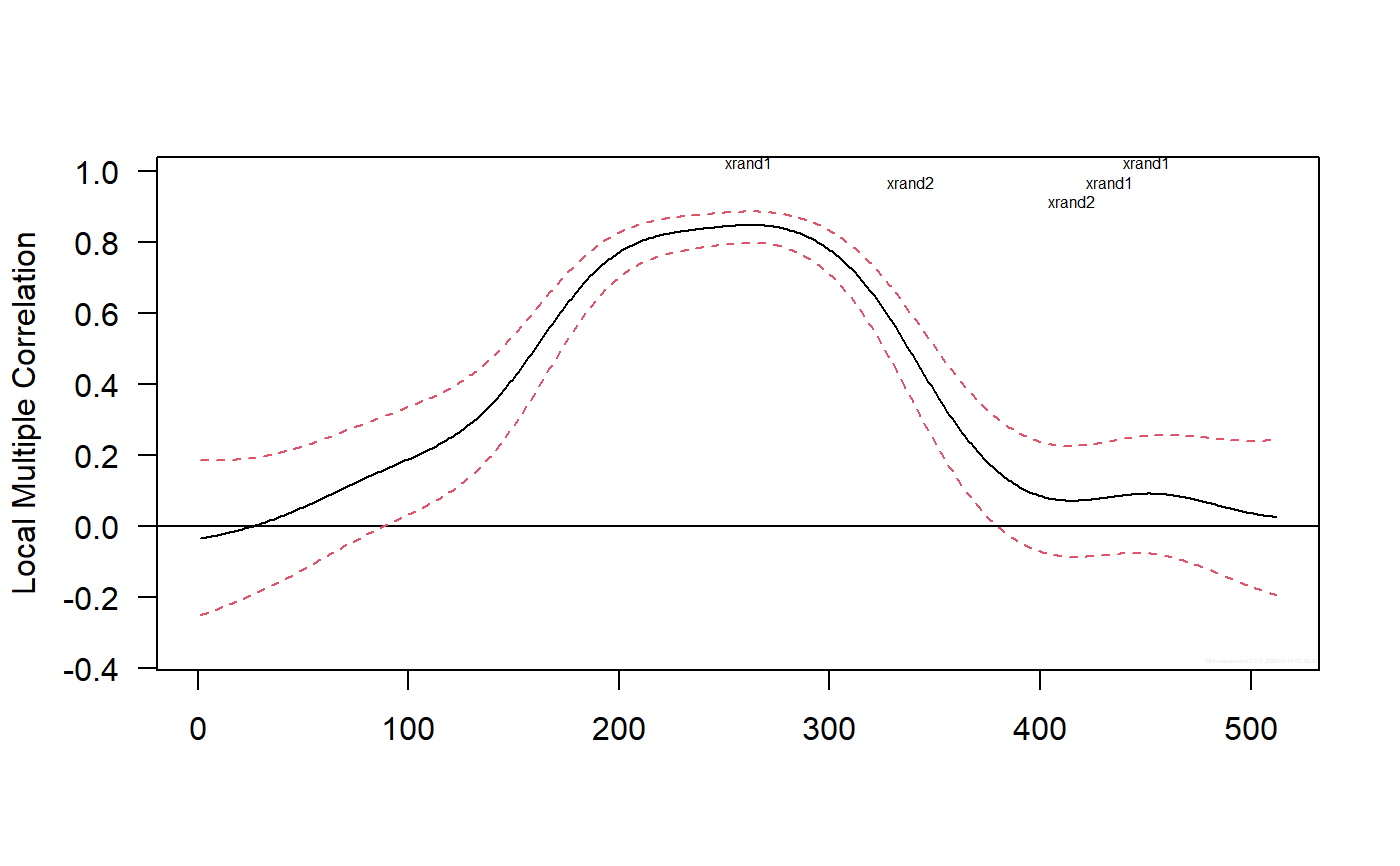
## Based on  Figure 4 showing correlation structural breaks in Fernandez-Macho (2018).

library(wavemulcor)
options(warn = -1)

xrand1 <- wavemulcor::xrand1
xrand2 <- wavemulcor::xrand2
N <- length(xrand1)
b <- trunc(N/3)
t1 <- 1:b
t2 <- (b+1):(2*b)
t3 <- (2*b+1):N

wf <- "d4"
M <- N/2^3 #sharper with N/2^4
window <- "gaussian"

J <- trunc(log2(N))-3

# ---------------------------

cor1 <- cor(xrand1[t1],xrand2[t1])
cor2 <- cor(xrand1[t2],xrand2[t2])
cor3 <- cor(xrand1[t3],xrand2[t3])
cortext <- paste0(round(100*cor1,0),"-",round(100*cor2,0),"-",round(100*cor3,0))

ts.plot(cbind(xrand1,xrand2),col=c("red","blue"),xlab="time")

xx <- data.frame(xrand1,xrand2)

# ---------------------------

Lst <- local.multiple.regression(xx, M, window=window) #, ymax=1)

# ---------------------------

##Producing correlation plot
plot_local.multiple.correlation(Lst)
#> NULL

##Producing regression plot
plot_local.multiple.regression(Lst)
#> NULL