Routine for local multiple cross-regression

Produces an estimate of local multiple cross-regressions (as defined below) along with approximate confidence intervals.

local.multiple.cross.regression(xx, M, window="gauss", lag.max=NULL, p=.975, ymaxr=NULL)

Arguments

xx	A list of \(n\) time series, e.g. xx <- list(v1, v2, v3)
M	length of the weight function or rolling window.
window	type of weight function or rolling window. Six types are allowed, namely the uniform window, Cleveland or tricube window, Epanechnikov or parabolic window, Bartlett or triangular window, Wendland window and the gaussian window. The letter case and length of the argument are not relevant as long as at least the first four characters are entered.
lag.max	maximum lag (and lead). If not set, it defaults to half the square root of the length of the original series.
p	one minus the two-sided p-value for the confidence interval, i.e. the cdf value.
ymaxr	index number of the variable whose correlation is calculated against a linear combination of the rest, otherwise at each wavelet level lmc chooses the one maximizing the multiple correlation.

Details

The routine calculates a set of time series of multiple cross-regressions, one per lagand lead) out of \(n\) variables.

Value

List of four elements:

cor:

List of three elements:

vals: numeric matrix (rows = #observations, cols = #lags and leads) providing the point estimates for the local multiple cross-correlation. lower: numeric vmatrix (rows = #observations, cols = #lags and leads) providing the lower bounds from the confidence interval. upper: numeric matrix (rows = #observations, cols = #lags and leads) providing the upper bounds from the confidence interval.

reg:

List of seven elements:

rval: numeric array (1st_dim = #observations, 2nd_dim = #lags and leads, 3rd_dim = #regressors+1) of local regression estimates. rstd: numeric array (1st_dim = #observations, 2nd_dim = #lags and leads, 3rd_dim = #regressors+1) of their standard deviations. rlow: numeric array (1st_dim = #observations, 2nd_dim = #lags and leads, 3rd_dim = #regressors+1) of their lower bounds. rupp: numeric array (1st_dim = #observations, 2nd_dim = #lags and leads, 3rd_dim = #regressors+1) of their upper bounds. rtst: numeric array (1st_dim = #observations, 2nd_dim = #lags and leads, 3rd_dim = #regressors+1) of their t statistic values. rord: numeric array (1st_dim = #observations, 2nd_dim = #lags and leads, 3rd_dim = #regressors+1) of their index order when sorted by significance. rpva: numeric array (1st_dim = #observations, 2nd_dim = #lags and leads, 3rd_dim = #regressors+1) of their p values.

YmaxR:

numeric matrix (rows = #observations, cols = #lags and leads) giving, at each value in time, the index number of the variable whose correlation is calculated against a linear combination of the rest. By default, lmcr chooses at each value in time the variable maximizing the multiple correlation.

data:

dataframe (rows = #observations, cols = #regressors) of original data.

References

Fernández-Macho, J., 2018. Time-localized wavelet multiple regression and correlation, Physica A: Statistical Mechanics, vol. 490, p. 1226--1238. <DOI:10.1016/j.physa.2017.11.050>

Examples

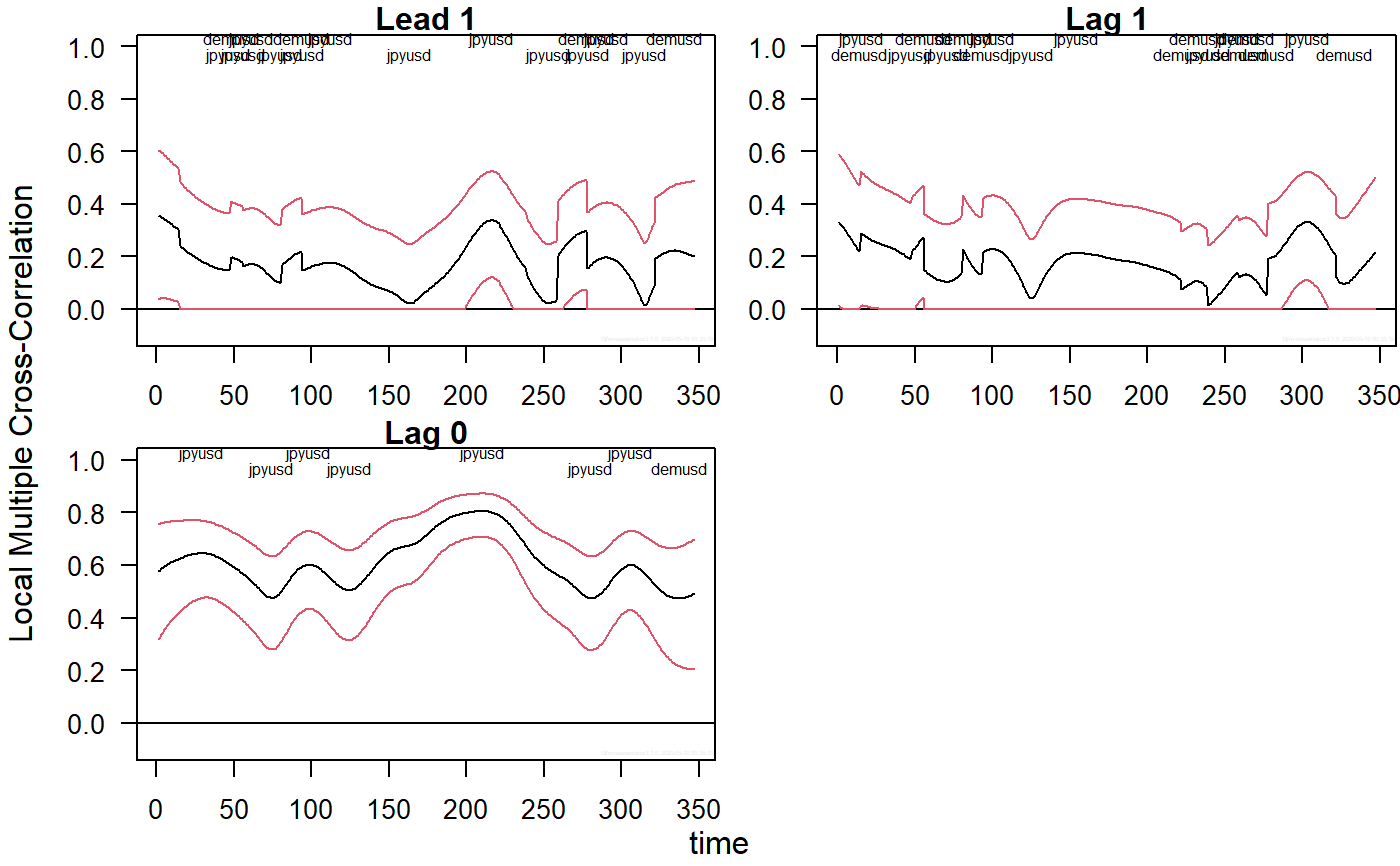
## Based on Figure 4 showing correlation structural breaks in Fernandez-Macho (2018).

library(wavemulcor)
data(exchange)
returns <- diff(log(as.matrix(exchange)))
returns <- ts(returns, start=1970, freq=12)
N <- dim(returns)[1]

M <- 30
window <- "gauss"
lmax <- 1

demusd <- returns[,"DEM.USD"]
jpyusd <- returns[,"JPY.USD"]

set.seed(140859)

xrand <- rnorm(N)

# ---------------------------

xx <- data.frame(demusd, jpyusd, xrand)
##exchange.names <- c(colnames(returns), "RAND")

Lst <- local.multiple.cross.regression(xx, M, window=window, lag.max=lmax)

# ---------------------------

##Producing correlation plot

plot_local.multiple.cross.correlation(Lst, lmax) #, xaxt="s")
#> NULL

##Producing regression plot

plot_local.multiple.cross.regression(Lst, lmax) #, nsig=2, xaxt="s")
#> NULL